CNFgen - graph formats

View on GitHub

CNFgen

Combinatorial benchmarks for SAT solvers

Download this project as a .zip file Download this project as a tar.gz file

The structure of some formula recipes in cnfgen is based on graphs, which can be either simple undirected graphs, biparite graphs, directed graphs or dag (directed acyclic graphs). It is possible either to read graphs from files or to generate them internally. The cnfgen tool accepts and saves graphs in the following file formats.

Different file formats are suitable for specific graph types, as shown in this table.

Graph type Description GML DOT KTH lists DIMACS Matrix
simple simple undirected graph Yes Yes Yes Yes No
digraph directed graph Yes Yes Yes Yes No
dag directed acyclic graph Yes Yes Yes No No
bipartite bipartite graphs Yes Yes Yes No Yes

If the file ends with one of the extensions .kthlist, .gml, .dot, .matrix, .dimacs then the program assumes that the file is the corresponding format, otherwise it is always possible in the command line to add the file format before the file name to avoid ambiguity. This is particularly useful when the graph is read from standard input or written on the standard output, or when the file extension does not match its file format.

Encoding

cnfgen assumes that given graph files encoded as UTF-8. Likewise it saves graph files in UTF-8 by default. In practice the output is ASCII unless some explicit non-ASCII commentary text or vertex/edge properties has been attached to the graph.

GML and DOT format — bipartite graphs representation

The convention adopted to specify bipartite graphs in DOT and GML formats is that to use a simple graph, where each vertex has either the attribute bipartite=0 or the attribute bipartite=1 set. This is the same convention used by graph library NetworkX.

KTH adjacency list format

[ Full specification by Jakob Nordström ]

The kthlist adjacency list graph format has been introduced by Jakob Nordström of the Proof Complexity research group at KTH Royal Institute of Technologyas as an efficient and simple way to represent sparse graphs for applications in SAT solving and proof complexity.

The format can specify all four types of graph, but the exact interpretation of the file depends a bit on the context.

KTH predecessors list format — digraph

The kthlist format as a straightforward interpretation as a directed graph, as described in the format specification.

KTH adjacency list format — dag

When CNFgen expects a directed acyclic graph, it expects the file in kthlist format to express very explicitly the topological order of the vertices. Namely the sequence of \(1\),… ,\(n\) is expected to be a topological order from sources to sinks of the vertices, and formula constructions in CNFgen will respect this order.

KTH predecessors list format — simple

For the file to represent a simple graph, a vertex \(v\) is listed in the adjacency list of \(u\) if and only if \(u\) is listed in the adjacency list of \(v\). If that is not the case, the file is considered invalid. Nevertheless CNFgen is more liberal and consider an edge \(\{u,v\}\) to be in graph when: (1) \(u\) is in the list of \(v\), or (2) when \(v\) is in the list of \(u\), or (3) both. Naturally all simple graphs generated by CNFgen are correct kthlist files according to the strictest interpretation of the format.

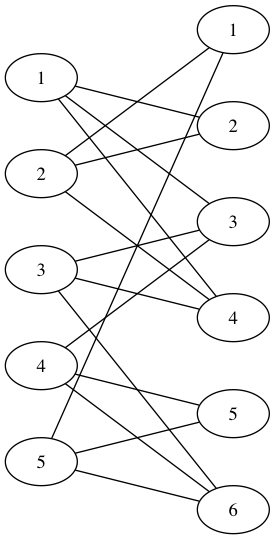
Here’s an example of how a graph with missing inverted edges is interpreted as an undirected graph. The file 

c
c This is a DAG of 5 vertices
c
5
1  : 0
2  : 0
3  : 1  0 
4  : 2  3  0  
5  : 2  4  0

represents the directed acyclic graph

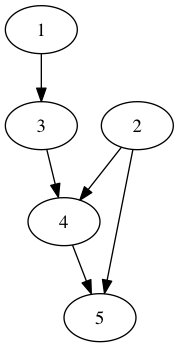
adjformatDAG.png

and the simple undirected graph

adjformatS.png

KTH predecessors list format — bipartite

The interpretation of a file as a bipartite graph is similar to the one for undirected graphs, with the difference that the bipartition is made explicit by listing just the adjacency lists of the vertices on the left side. It should be stressed that any isolated vertex on the left side must be listed with its zero neighbors otherwise its position would be ambiguous. CNFgen expects all vertices on the left side to be listed in order, without skipping any of them. The neighborhood can be specified in any order, which will be preserved and taken in account. 

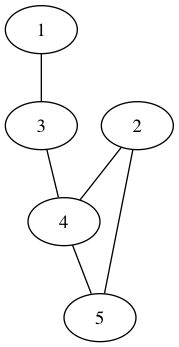
c listing only left side vertices (bipartite graph)
11
1 : 7  8  9 0
2 : 6  7  9 0
3 : 8  9 11 0
4 : 8 10 11 0
5 : 6 10 11 0

The difference with the undirected graph is specification is important. Notice that according to the format spec the previous example is not a correct kthlist file for an undirected graph because it lacks the adjacency lists of the right side vertices too. The following is the same graph, but encoded as an undirected graph and it is not in the correct format when a biparite graph is expected. 

c listing left and right side vertices (undirected graph)
11
1 : 7  8  9 0
2 : 6  7  9 0
3 : 8  9 11 0
4 : 8 10 11 0
5 : 6 10 11 0
6 : 2  5  0
7 : 1  2  0
8 : 1  3  4 0
9 : 1  2  3 0
10 : 4 5 0
11 : 3 4 5 0

kthformatBI.png

Matrix format

The matrix format is suitable to represent the adjacency matrix of a bipartite graph, where rows correspond to vertices on the left side and columns to vertices on the right side.

The file consists on two numbers r and c separated by whitespace, followed by a whitespace separated sequence of zeros and ones of length \(r\times c\). Here's a well formatted example. 

5 6
0 1 1 1 0 0
1 1 0 1 0 0
0 0 1 1 0 1
0 0 1 0 1 1
1 0 0 0 1 1

which represents the bipartite graph

matrixformatEG.png